Как найти среднее арифметическое

Объясним, как вычислить среднее арифметическое набора чисел, почему это важно в статистике и ежедневной жизни.

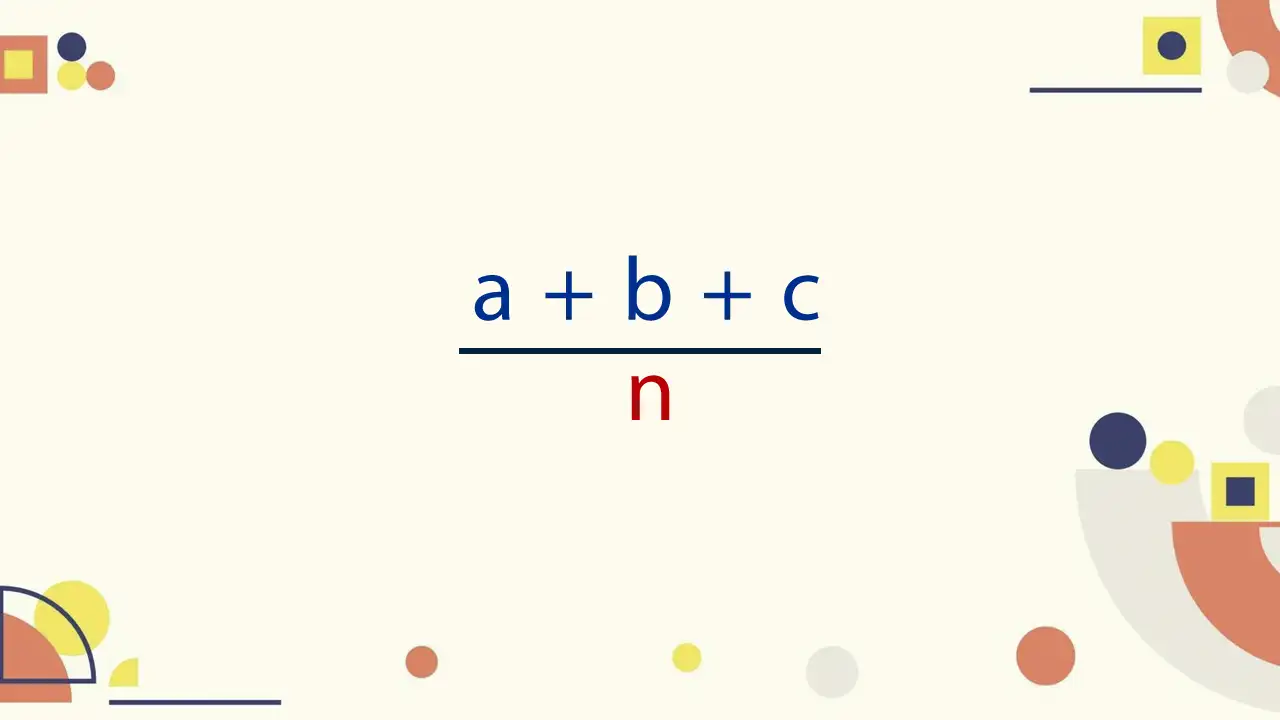
Среднее арифметическое помогает нам понять общие тенденции из набора данных. Изучив следующие разделы, вы сможете легко ориентироваться в различных типах средних значений:

• Определение среднего арифметического: простое объяснение
• Пошаговое руководство с примерами, как вычислить среднее арифметическое
• Среднее арифметическое взвешенное и его практическое применение
• Что такое среднее геометрическое и его значение в анализе данных
• Обзор других мер центральной тенденции: медиана, мода и другие

Что такое среднее арифметическое?

Среднее арифметическое - это статистический показатель, который определяет среднее значение набора чисел. Это один из самых распространённых методов для выражения «типичного» значения в группе.

🔍 Простой пример. Если у вас есть пять яблок, весом 100, 120, 80, 90 и 110 грамм, то средний вес яблока можно вычислить, сложив все веса и разделив сумму на количество яблок. Результат - среднее арифметическое:

(100 + 120 + 80 + 90 + 110) / 5 = 100 грамм

Это значение помогает понять, какой вес имеют яблоки «в среднем», что особенно полезно в ситуациях, когда нужно сделать обобщение или сравнение.

📊 Значение в статистике. Среднее арифметическое используется не только в повседневной жизни, но и в научных исследованиях, экономике, бизнесе, в расчете скоростей, и многих других областях для анализа данных.

Однако, среднее арифметическое может быть не всегда показательным, если в данных есть очень большие или маленькие значения, которые искажают общий результат. В таких случаях могут использоваться другие статистические меры, такие как медиана или мода.

Как вычислить среднее арифметическое: пошаговое руководство с примерами

Вычисление среднего арифметического - это базовый навык, который пригодится во многих жизненных ситуациях. Оно поможет вам оценить общие тенденции и сделать информированные решения.

Для начала, давайте рассмотрим, что вам понадобится:

• Набор чисел, для которых вы хотите найти среднее.
• Доступ к базовому калькулятору или умение выполнять простые арифметические операции.

🧮 Шаг 1. Суммирование всех чисел. Первым делом, сложите все числа в вашем наборе. Это даст вам их общую сумму.

👥 Шаг 2. Подсчет количества чисел. Определите, сколько чисел содержится в вашем наборе. Это количество будет делителем.

➗ Шаг 3. Деление суммы на количество. Разделите общую сумму чисел на их количество. Результат этого деления и будет вашим средним арифметическим.

Среднее арифметическое = Сумма чисел / Количество чисел

Давайте рассмотрим пример:

1. Числа: 5, 15, 10, 20, 5.
2. Сумма: 5 + 15 + 10 + 20 + 5 = 55.
3. Количество чисел: 5.
4. Среднее арифметическое: 55 / 5 = 11.

В этом примере среднее арифметическое пяти чисел равно 11. Это означает, что "в среднем" каждое число приблизительно равно 11.

🔍 Важно помнить. Среднее арифметическое не всегда является идеальным показателем. Например, если ваши данные содержат очень высокие или низкие значения, они могут сильно исказить среднее. В таких случаях рассмотрите использование других статистических мер.

Что такое среднее арифметическое взвешенное и его практическое применение

Среднее арифметическое взвешенное является ещё одним методом расчёта среднего значения, который позволяет учитывать различное весовое значение элементов набора данных.

Прежде чем мы перейдем к объяснению и примерам, важно понять одну вещь:

Робастность - это свойство статистических методов быть устойчивыми к аномалиям в данных. Среднее арифметическое не является робастным показателем, так как сильно подвержено влиянию экстремальных значений.

Например, в районе с высокими доходами один миллиардер может сильно исказить расчёт среднего дохода, делая его неотражающим реальное положение дел.

Пример набора данных: 1, 2, 2, 2, 3, 9

Среднее арифметическое этих данных равно 3.17, что выше большинства значений набора.

🔑 Как это работает. В среднем арифметическом взвешенном каждому значению присваивается определённый вес, и среднее вычисляется с учётом этих весов.

Это особенно полезно, когда некоторые данные более значимы или релевантны для исследования, чем другие.

1. Шаг 1. Определите веса для каждого значения в вашем наборе данных.
2. Шаг 2. Умножьте каждое число на его вес.
3. Шаг 3. Сложите все полученные произведения.
4. Шаг 4. Сложите все веса.
5. Шаг 5. Разделите сумму произведений на сумму весов.

Для примера вы пожете посмотреть калькулятор расчета среднего взвешенного балла в зависимости от количества учебных часов предмета.

Такой подход минимизирует искажение среднего значением с экстремальными весами и даёт более точное представление о данных.

В качестве заключения, понимание различных типов средних значений и их применение может значительно повысить точность ваших статистических выводов и аналитических решений.

Что такое среднее геометрическое и его значение в анализе данных

Среднее геометрическое - это еще один метод оценки центральной тенденции, который особенно полезен при работе с пропорциональными и логарифмическими данными.

Этот метод находит широкое применение в финансах, биологии и других областях, где важно учесть рост или изменение в процентном выражении.

Среднее геометрическое - это n-ый корень из произведения n чисел. Это среднее значение, которое показывает типичный элемент ряда данных, умноженных друг на друга.

🔢 Пример. Если у вас есть рост цен на товары за 4 года на 10%, 20%, 15% и 5%, то среднее геометрическое поможет оценить средний процент изменения цен в каждом году.

1. Шаг 1. Перемножьте все процентные ставки вместе.
2. Шаг 2. Извлеките корень четвертой степени (поскольку у нас 4 значения) из полученного произведения.

Среднее геометрическое = √√√√(1.1 * 1.2 * 1.15 * 1.05)

Этот метод обеспечивает более реалистичное представление о среднем росте, поскольку он учитывает эффект компаундинга (сложного процента).

📉 Важность. Среднее геометрическое часто более информативно, чем арифметическое, когда дело доходит до анализа изменений, которые происходят через равные промежутки времени.

Оно помогает увидеть «настоящий» рост или снижение, исключая возможное искажение, которое могут вызвать аномально высокие или низкие значения в арифметическом расчете.

Таким образом, использование среднего геометрического может дать более точное и честное представление о том, что происходит с вашими данными во времени.

Другие средние: медианы, моды и другие меры центральной тенденции

Помимо среднего арифметического, существует множество других статистических мер, которые помогают анализировать данные. Каждая из них имеет свои преимущества и подходит для разных сценариев.

Важно помнить, что среднее арифметическое не всегда является робастным показателем. Это означает, что оно может быть чрезмерно чувствительным к выбросам или экстремальным значениям в наборе данных, искажая общий вывод.

📉 Робастность среднего арифметического. Напомним, что значительные отклонения в данных могут значительно повлиять на среднее арифметическое, делая его менее надежным для некоторых аналитических задач.

Медиана - это тип среднего, который указывает центральное значение набора данных. Она разделяет данные на две равные части: одна половина данных меньше медианы, другая - больше.

Мода - это значение в наборе данных, которое встречается чаще всего. Мода может быть полезна в анализе категориальных данных или данных с повторениями.

🔍 Примеры использования.

• Медиана часто используется для анализа доходов, потому что она менее чувствительна к очень высоким или низким значениям, которые могут исказить среднее.
• Мода может быть полезна для определения наиболее распространенного цвета в выборке одежды или наиболее популярного товара в продажах.

Важно отметить, что иногда в данных может быть более одной моды, что делает их бимодальными или даже мультимодальными, что тоже важно для анализа.

💡 Совет. Чтобы выбрать подходящую меру центральной тенденции, важно понимать природу и распределение ваших данных, а также цели анализа.

Используя различные меры центральной тенденции, вы сможете получить более полное и точное представление о ваших данных, улучшая таким образом качество вашего исследования или анализа.

Есть что добавить?

Напишите своё мнение, комментарий или предложение.