Оглавление:
Что такое корень числа?
Корень n-й степени из числа x — это такое число r, которое в степени n равняется x. Или другими словами: rn= x.
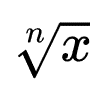
Эта запись с математическим корнем из числа х в n-ой степени имеет собственное название в каждом символе:
- n — здесь является степенью или показателем корня, n всегда является натуральным числом, таким, как — 1, 2, 3 и так далее.
- х — здесь является выражением или подкоренным числом. Выражается, как вещественное или любое комплексное число.
- √ — здесь является символом корня или знаком, имеющим еще другое название — радикал.
Например:
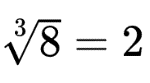
Такое выражение читается, как корень третьей степени от числа 8. Это корень равняется двум. Число 3 здесь является степенью корня, а число 8 – подкоренным числом.
В математике нахождение корня называется «извлечение корня».
Причём важно разделять понятия арифметического и алгебраического корня.
Арифметический или алгебраический (общий)
Арифметический корень n-й степени из неотрицательного вещественного числа a — это неотрицательное число b, для которого bn=a. Обозначается арифметический корень знаком радикала (про который мы уже сказали выше).
Арифметический корень второй степени из числа a (√a) — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a. К примеру, корнями второй степени из числа 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
Таким образом, арифметический корень, в отличие от корня общего вида (или алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно и неотрицательно.
Далее мы будем говорить именно про арифметические корни.
Наиболее часто используемые корни — это корни второй степени и корни третьей степени. Они даже имеют собственные названия:
- Квадратный корень
- Кубический корень
Квадратный корень
Квадратный корень – это корень со степенью два. Чаще всего, в значении радикала степень «два» не прописывается, а просто используется символ √.
Арифметический квадратный корень всегда является положительным числом, и кроме того подкоренное значение также всегда положительно.
Почему все происходит именно так, нам расскажет простой пример с решением:
- Ищем квадратный корень из -16.
- Логично предположить в ответе - 4.
- Но если проверить таким образом: 4*4 = 16 — то нет, не сходится.
- Если - 4, то -4 * -4 = 16, нужно отметить, что минус на минус всегда в итоге дает плюс.
Ни одно число при возведении его в квадрат не дает отрицательного результата.
Вывод: все числа, которые стоят под знаком корня, всегда должны быть положительными.
Кубический корень
Кубический корень – это такое число, которое для получения подроренного числа нужно умножить само на себя три раза.
К примеру, кубический корень из 64 будет равен «4».
Решение будет выглядеть так: 4х4х4 = 64.
Как появились математические корни?
Впервые задачи, в которых извлекался квадратный корень, обнаружили у вавилонских математиков. Именно в них применялись теоремы Пифагора для того, чтобы определить треугольник с прямыми углами по двум другим известным сторонам.
Также в них находили стороны квадрата с заданной площадью и решали квадратные уравнения.
Для извлечения квадратного корня древние математики разработали специальный численный метод. Для квадратного корня из «a» они рассчитывали натуральные числа n в меньшую сторону из ближайшего к корню. Если выражение «a = n2 + r» представить в таком виде, то можно получить
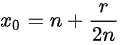
И далее шел уточняющий процесс, который соответствовал методу Ньютона:
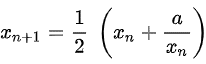
Как произошла символика значений? У корня очень сложная и долгая история. Его извлекали еще древние греки и подходили к этому очень ответственно: они находили стороны квадрата по его площади. Математики средневековья сокращали корень от «radix» и обозначали его Rx.
В современном понятии черта над подкоренным выражением сначала отсутствовала, но в 1637 году ее ввел Декарт вместо скобок. Сейчас она так и осталась со знаком корня.
Рене Декарт (1596–1650) — французский математик и философ. Декарт является одним из основателей философии Нового времени и аналитической геометрии, а ещё он – одна из ключевых фигур научной революции.
Главные свойства корней
Корень нечетной степени, состоящий из положительного числа — есть положительное число, определенное однозначно.
Корень нечетной степени, состоящий из отрицательного числа — есть отрицательное число, определенное однозначно.
Корень чётной степени, состоящий из положительного числа, имеет 2 значения со знаками противоположности, но равными по модулю.
Корень чётной степени, состоящий из отрицательного числа в области вещественных чисел, не существует, так как при возведении любого вещественного числа в степень с четными показателями в результате получится неотрицательное число.
Ниже показано, как извлекать данные корни в множестве комплексных чисел, когда значениями корня будут n комплексных чисел.
Корень любой натуральной степени из нуля — ноль.
Алгоритм нахождения корня n-степени
Корень n-ой степени n√A действительного положительного числа А есть действительное положительное решение уравнений xn = A.
Как найти быстро сходящийся алгоритм корня в n-ой степени? Для этого нужно:
1. Вычислить начальное предположение x0
2. Определить
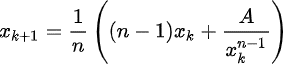
3. Далее повторять пункт № 2 до момента, пока необходимая точность не будет достигнута.
Для нахождения квадратного корня итерационной формулы Герона служит частный случай, с подстановкой выглядит так:
n = 2 в шаг 2: xk+1 = (xk + A/xk) / 2
Имеется несколько вариантов данного алгоритма. Один - как касательный метод Ньютона для нахождения нулей функций f(x). Сходится такой метод достаточно быстро, несмотря на то что является итерационным.
У этого метода скорость сходимости является квадратичной. Это указывает на то, что числа с верными разрядами в ответе будут удваиваться с каждой итерацией — другими словами, будет увеличиваться точность нахождения ответа с 1-го до 64-х разрядов, и будет требоваться только шесть итераций. Но следует помнить и о машинной точности.
Из всего этого можно сделать заключение, что в компьютерах данный алгоритм используется, как самый быстрый метод нахождения корней в квадрате.
Что касается больших значений n, то алгоритм здесь будет менее эффективным, поскольку потребует на каждом шагу таких вычислений:
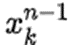
Но такое вычисление выполняется при помощи алгоритма быстрого возведения в степень.
❓Вопросы и ответы
А также обратите внимание на ответы на некоторые часто задаваемые вопросы.
Для чего на практике надо найти корень?
Если в науке что-то существует - то это обязательно для чего-то нужно, даже если нет обычного понимания для чего. Квадратный корень используется повсюду, но в основном там, где имеется какая-нибудь геометрия.
К примеру, компьютерная графика. Для значительного достижения и улучшения в свое время применялись специальные алгоритмы быстрого обратного квадратного корня в играх. Сегодня без квадратных корней невозможно поиграть в такие игры, как «танчики», Скайрим, Киберпанк.
Можно ли корень записать в виде степени?
Да, корень от x в степени n – это x в степени 1/n.
Как связаны между собой степень в виде десятичной дроби и корни?
Переход от степени с выражениями и дробными показателями в основании выполняется на области всех допустимых значений в основании степени при исходных выражениях.
К примеру:
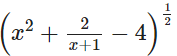
представляется, как квадратный корень
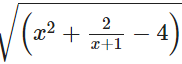
А запись
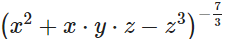
выражается для всех x, y, z, как
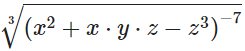
Как пользоваться калькулятором корней?
Для того, чтобы вычислить квадратный корень с пошаговым объяснением, достаточно воспользоваться калькулятором на этом сайте ecalc.ru.
Наш сайт позволяет быстро и точно вычислить корень из числа онлайн. И не нужно высчитывать все самостоятельно в уме, искать готовые решения задач или проверять ответы.
Нужно просто вписать все необходимые данные. Если нужно просто найти корень, следует указать число под √. Если понадобится, то ввести степень. Обычно вычисляется корень во второй степени, но здесь ее можно и не указывать.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Индикт - что это и чему он равен. Индикт — это средневековый период времени, равный 15 годам.
- Декада - это сколько дней. Декада состоит из 10 дней, калькулятор показывает количество дней в декаде.
- Сколько лет в тысячелетии. Введите количество тысячелетий, чтобы узнать, сколько в них лет.
- Сколько месяцев в веке. Введите количество веков, чтобы узнать, сколько в них месяцев.
- Перевести месяцы в года. Введите количество месяцев, калькулятор переведет их в года.
- Перевести годы в недели. Введите количество лет, калькулятор переведет их в недели.
- Перевести недели в дни. Введите количество недель, калькулятор переведет их в дни.
- Перевести дни в недели. Введите количество дней, калькулятор переведет их в недели
- Перевести академические часы в часы. Введите количество академических часов, калькулятор переведет их в часы.
- Перевести наносекунды в миллисекунды. Введите количество наносекунд, калькулятор переведет их в миллисекунды.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии