Бросить монетку

Зачем подбрасывают монетку?

Подбрасывание монеты – это действие, которое достаточно часто используется в повседневной жизни, как теория вероятности при «генерации случайностей».

Для того чтобы подбросить монетку, необходимо совершить действие, которое очень часто в повседневной жизни и в теории вероятности выступает, как генератор некой случайности. При этой теории монетка может выдавать такие позиции, как орёл и решка:

Орёл

Решка

В качестве развлечения могут использоваться две монеты, а также три монеты по нескольку раз. Эти действия с монетками могут понадобиться при необходимости принять какое-либо решение из двух разных вариантов, как правило, это может возникать при различных спорах. Также подбрасывать монетку можно во время игры, типа орлянки или при жеребьевке разных видов спорта, например, перед футбольным матчем.

При подкидывании монеты всегда очень важны именно ее вращательные движения и колебания, а также при падении в конце траектории вероятность ее отскока.

Американские математики продемонстрировали наличие определенной методики, которая позволяет бросить монетку таким образом, чтобы она не переворачивалась в воздухе. Внешне такой бросок будет совершенно обычным. Но если овладеть определенным мастерством и хорошенько потренироваться, то данный прием можно использовать при работе с фокусами или в каких-то профессиональных играх. Иногда при броске монетка может вставать на ребро, но это происходит достаточно редко.

Примеры использования подбрасывания монеты

Вот ещё несколько примеров использования подбрасывания монеты в жизни.

🦅 Игра «Орлянка»

Смысл данной игры достаточно прост. Необходимо подкинуть монету и смотреть на то, как она упала. Если сверху на монете окажется изображение орла, то выиграет первый бросивший игрок, если будет изображение решки - то победу одержит, соответственно, второй игрок. При падении монетки всегда существует почти 100% вероятность того, что монетка упадет на одну из сторон, а не встанет на ребро.

🪙 Игра «Ту-ап»

В этой игре сначала игроками и зрителями делаются ставки на какую-либо комбинацию, после чего игрок занимает позицию в центре круга со специальной дощечкой в руках. На этой дощечке находятся две монеты. Одна из них лежит кверху «решкой», а другая - «орлом».

Игрок начинает подкидывать с дощечки монеты и если обе выпадут в позиции «орёл», то этот игрок выиграл, а если в комбинации будет одна «решка» и один «орёл», то участник должен сделать еще один бросок. В случае, если выпадет две «решки» - игрок проиграл и должен передать ход следующему участнику.

За процессом соблюдения всех правил, а также за ставками в игре следит специальный арбитр.

⚽ Перед футбольным матчем

Перед началом матча рефери подбрасывает монетку для того, чтобы определить прерогативу по введению мяча в игру и определить какая из команд первой будет начинать игру с центрального круга, а какая - с ворот.

Монетка с помощью изображения решки или орла способна решить исход этого судьбоносного жребия в матче. По сути, монетка является очень важным атрибутом каждого судьи. Зачастую наличие эффективного подкидывания монетки является хорошим фундаментом для победы команды, которая угадает правильную сторону.

🧘 Техника «Прояснение чувств»

Данная техника приписывается Зигмунду Фрейду. Она необходима для оказания помощи в принятии каких-то трудных решений. Заключается в подбрасывании монеты не для самого определения решения, а для того, чтобы прояснить именно чувства того лица, которое принимает решение.

Зигмунд Фрейд объяснял свои доводы так: "Вы не должны всегда слепо следовать тому, что говорит монета. Вы должны обратить внимание на что она указывает, а уже после этого проследить за своими собственными реакциями. Вы должны спросить сами себя: доволен ли я всем этим? А может быть я разочарован?»

Именно это, по словам знаменитого психолога, помогает понять, как человек на самом деле относится к тому или иному вопросу глубоко внутри себя.

Взяв это за основу, такой человек всегда будет готов прийти к верному умозаключению и принять правильное решение.

🤔 Задачи с монеткой на вероятность

Для таких задач отлично подходят формулы, по которым определяется вероятность:

m / n = P

n - является числом исходов с подбрасыванием монеты;

m - число исходов, благоприятных какому-то событию.

А как именно определить эти исходы?

Для этого нужно два раза бросить монету и найти вероятность того, что орёл выпадет именно 1 раз.

• P — это решка
• О — это орёл

Формула выпадения записывается в таком виде: РР, ОР, РО, ОО.

Это говорит о том, что выпало 2 решки, после этого орёл+решка, затем решка+орёл, а в конце - 2 орла. При подсчете данной комбинации получается n - 4.

Далее определяются только те комбинации, которые подходят под условие, где орёл выпадает только 1 раз. Вот эти комбинации: ОР и РО.

В итоге получается m - 2.

Таким образом формула вероятности будет выглядеть так: P=2/4=1/2=0.5

🎲 Ошибка игрока и ложный вывод Монте-Карло

Очень часто людям кажется, что предыдущие подбрасывания каким-то волшебным образом влияют на все последующие. То есть, если, например, 5 раз подряд выпала решка, то создается впечатление, что вероятность выпадения орла в 6 раз выше, хотя на самом деле она равна 50%, так как сами события между собой совершенно независимы.

Ошибка игрока подразумевает под собой неверное понимание череды событий, дающих убеждение в том, что будущие отклонения в противоположном направлении становятся более вероятными. Но тогда каждое событие следует рассматривать в отдельности не как в цепи событий, а как статистически независимые от предыдущих событий.

Реальные эксперименты с подбрасыванием монеты

Существует мнение, что при многократном подбрасывании монеты выпадет примерно одинаковое количество орлов и решек (50х50). Но достоверные опыты Жоржа-Луи Леклерка и графа де Бюффона доказывают, что такая вероятность может отклоняться. И это неудивительно, ведь подкидывание монетки — это независимые и совершенно случайные события.

Ниже показана таблица с результатами опытов де Бюффона в играх.

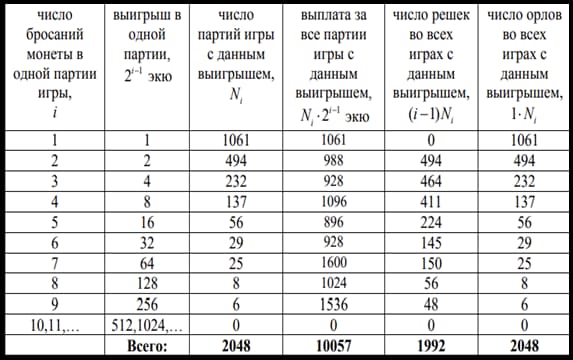
По предположению графа, нормальная плата, например, за одну партию игры должна быть примерно 5 экю, а не огромной суммой, как показывает теория вероятности.

Для обоснования этого вывода де Бюффон выдвинул остроумные аргументы, которые, надо признать, были с формально математической точки зрения ошибочными и содержали идеи относительно практической невозможности наступления событий самой минимальной вероятности и полезности денег.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Индикт - что это и чему он равен. Индикт — это средневековый период времени, равный 15 годам.
• Декада - это сколько дней. Декада состоит из 10 дней, калькулятор показывает количество дней в декаде.
• Сколько лет в тысячелетии. Введите количество тысячелетий, чтобы узнать, сколько в них лет.
• Сколько месяцев в веке. Введите количество веков, чтобы узнать, сколько в них месяцев.
• Перевести месяцы в года. Введите количество месяцев, калькулятор переведет их в года.
• Перевести годы в недели. Введите количество лет, калькулятор переведет их в недели.
• Перевести недели в дни. Введите количество недель, калькулятор переведет их в дни.
• Перевести дни в недели. Введите количество дней, калькулятор переведет их в недели
• Перевести академические часы в часы. Введите количество академических часов, калькулятор переведет их в часы.
• Перевести наносекунды в миллисекунды. Введите количество наносекунд, калькулятор переведет их в миллисекунды.

Поделитесь в соцсетях

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.