Калькулятор квадратных уравнений

Решение квадратных уравнений

Квадратные уравнения начинают разбирать в 8-м классе средней школы. В их решении нет ничего трудного. В интернете существует много разных онлайн площадок, где для решения данных уравнений на помощь придет подходящий калькулятор.

Квадратные уравнения – это алгебраические действия, имеющие 2-ю степень общего вида:

a·x² + b·x + c = 0

Коэффициентами здесь будут являться производные: a, b, c, и a ≠ 0.

В начале изучения всех существующих способов вычислений, следует отметить, что квадратные уравнения разделяются на три вида:

1. Без корня;
2. Имеющий только один корень;
3. Имеющий 2 разных корня.

Метод определения корней

Чтобы вычислить то, сколько имеется корней в уравнении, следует воспользоваться дискриминантом.

Дискриминант

У уравнения a·x² + b·x + c = 0 дискриминант является обычным: D = b² − 4ac.

Представленную формулу желательно хорошенько выучить. Совершенно не важно ее происхождение. Основным является то, сколько именно корней будет находиться в квадратном уравнении. Это определяется по дискриминанту.

Делается все следующим образом:

1. Если D < 0, корней нет;
2. Если D = 0, есть только один корень;
3. Если D > 0, будет два корня.

Очень важно учесть то, что дискриминант всегда говорит о том, сколько корней, а не обозначений.

Если обратиться к примерам, то все станет понятным:

Возьмем задачу именно на количество корней, имеющих квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

После чего запишем коэффициенты для 1-го уравнения и таким образом, определим дискриминант:

1. a = 1, b = −8, c = 12;
2. D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

В итоге мы получаем положительный дискриминант. Именно поэтому уравнение будет содержать два разных корня.

У другого уравнения решение точно такое же:

1. a = 5; b = 3; c = 7;
2. D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Здесь корней нет, а дискриминант отрицательный.

Сделаем еще один разбор:

1. a = 1; b = −6; c = 9;
2. D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Итог: Один корень, дискриминант равняется 0.

Также очень важно, чтобы коэффициенты были написаны к конкретному уравнению. Возможно это нудно и долго — но зато есть гарантия того, что никакие глупые ошибки не произойдут, а коэффициенты не перепутаются. И здесь нужно самостоятельно сделать ставку либо на скорость, либо на качество.

Если выработать определенную сноровку, то через какое-то время выписывать коэффициенты совсем не потребуется. Все эти манипуляции и вычисления будут спокойно выполняться в уме. Это будет происходить у большинства людей примерно после того, как будет решено около 70-ти уравнений. Согласитесь, что цифра не такая уж значительная.

Корни квадратного уравнения

Важнейшая формула корня квадратного уравнения при дискриминанте D > 0

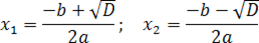
Если D = 0, то, пользуясь такими формулами, можно получить такое же число. Именно оно и будет являться ответом.

А если, например, D < 0 и корней нет, то считать больше не нужно.

Таким образом, когда есть знание формул и умение считать, то никаких проблем не будет. Обычно разного рода накладки могут появляться, когда в формулу подставляются отрицательные коэффициенты.

На помощь придет прием, когда нужно глядя на формулу перед собой, конкретно расписывать свои действия. Тогда можно быстро устранить все ошибки.

Неполные квадратные уравнения

Квадратные уравнения могут иметь отличия от определений. К примеру:

1. x² + 9x = 0;
2. x² − 16 = 0.

Видно, что в уравнениях нет одного слагаемого. Эти квадратные уравнения вычисляются намного легче, чем уравнения стандартного плана, потому что тут не нужно считать дискриминант.

Разберем положение:

Неполное квадратное уравнение: ax² + bx + c = 0,

где b = 0 или c = 0, то есть коэффициент или свободный элемент = 0 при переменной x.

Или в более сложном случае b = c = 0, где оба коэффициента = 0.

И тогда уравнение уже выглядит так: ax² = 0.

И у него единственный корень: x = 0.

Также следует изучить и другие способы:

Например: b = 0, и мы здесь получаем неполное квадратное уравнение: ax² + c = 0.

Если чуть-чуть его преобразовать, то получится:

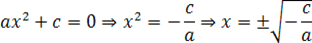
Решение неполного квадратного уравнения

Из-за того, что квадратный корень получается лишь из неотрицательного числа, то крайнее равенство имеет смысл только при (−c/a) ≥ 0.

На основании чего делаем заключение:

1) Когда в неполном квадратном уравнении: ax² + c = 0

есть неравенство (−c/a) ≥ 0, то получится два корня.

2) А когда (−c/a)< 0, то корней не будет.

Таким образом дискриминант нам даже не потребовался. В неполных квадратных уравнениях трудных вычислений нет.

Поэтому не нужно помнить неравенство (−c/a) ≥ 0. Можно указать величину x² и взглянуть, что находится с противоположной стороны от знака (=) равно.

Если какое-то положительное число — то в нем будет два корня.

Если какое-то отрицательное число — то корней здесь вообще не будет.

Далее необходимо разобраться с уравнением: ax² + bx = 0,

Здесь свободный элемент = 0. А значит будет всегда именно 2 корня.

Нужно только многочлен распределить на множители:

Если какой-то множитель = 0, то произведение тоже будет = 0.

Вычисление квадратных уравнений:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6.

Корни здесь отсутствуют, поскольку квадрат не является отрицательному числу равным.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.

Теорема Виета

Квадратное уравнение: x² + bx + c = 0.

Если здесь есть корни x1 и x2, то будут верны такие определения:

1) x1 + x2 = −b.

Здесь сумма корней квадратного уравнения равняется коэффициенту переменной x, который находится с противоположным знаком;

2) x1 · x2 = c.

В данном варианте произведение корней равняется свободному коэффициенту.

Например:

1. x² − 9x + 20 = 0 ⇒ x1 + x2 = − (−9) = 9; x1 · x2 = 20; корни: x1 = 4; x2 = 5;
2. x² + 2x − 15 = 0 ⇒ x1 + x2 = −2; x1 · x2 = −15; корни: x1 = 3; x2 = −5;
3. x² + 5x + 4 = 0 ⇒ x1 + x2 = −5; x1 · x2 = 4; корни: x1 = −1; x2 = −4.

Теорема Виета указывает на добавленную информацию о корнях квадратного уравнения. Кому-то она кажется немного трудной, но если чуть-чуть потренироваться, то корни можно вычислять очень быстро, и также быстро угадывать их.

Данная теорема способна упрощать решение квадратных уравнений. Поэтому ставим большое НЕТ каким-то трудным вычислениям, арифметическим корням и дробям. Нам не понадобился также и дискриминант.

Когда в результате решения получается «не хорошее» квадратное уравнение (коэффициент при x² отличается от 1-го), это исправляется очень легко — стоит только посмотреть на примеры выше.

Как решать квадратные уравнения по теореме?

Шаг 1. Всегда сводить квадратное уравнение к тому, которое приведено, но только если это не выполнено в условиях самой задачи.

Шаг 2. Если коэффициенты в квадратном уравнении являются дробными, решение осуществляется через дискриминант.

Шаг 3. Если коэффициенты целочисленные - решение происходит по теореме Виета.

Шаг 4. Если угадать корни в течение нескольких секунд не удалось, оставляем теорему Виета и делаем решение через дискриминант.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Индикт - что это и чему он равен. Индикт — это средневековый период времени, равный 15 годам.
• Декада - это сколько дней. Декада состоит из 10 дней, калькулятор показывает количество дней в декаде.
• Сколько лет в тысячелетии. Введите количество тысячелетий, чтобы узнать, сколько в них лет.
• Сколько месяцев в веке. Введите количество веков, чтобы узнать, сколько в них месяцев.
• Перевести месяцы в года. Введите количество месяцев, калькулятор переведет их в года.
• Перевести годы в недели. Введите количество лет, калькулятор переведет их в недели.
• Перевести недели в дни. Введите количество недель, калькулятор переведет их в дни.
• Перевести дни в недели. Введите количество дней, калькулятор переведет их в недели
• Перевести академические часы в часы. Введите количество академических часов, калькулятор переведет их в часы.
• Перевести наносекунды в миллисекунды. Введите количество наносекунд, калькулятор переведет их в миллисекунды.

Поделитесь в соцсетях

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.