Оглавление:
Что такое дроби?
Дробь– это число, которое состоит из нескольких одинаковых частей - долей единицы, а также из одной ее части.
Обыкновенная дробь выглядит так:
В математической записи дроби число, которое находится выше черты - называется числителем, а число, которое расположено ниже - называется знаменателем. Оно показывает то, на сколько долей разделили единицу.
Первое число является делимым, а второе число служит делителем. Обыкновенные дроби могут образовывать поле рациональных чисел, если они будут с целыми числителями и ненулевыми знаменателями. Они показывают количество долей, на которые делится единица.
Математические дроби начинают изучать в школе. В основном в 5 или в 6 классах. Но также дроби очень часто используются в дальнейшей школьной и затем в вузовской программах.
История дробей
Русское слово «дробь», как и его аналоги в других языках, происходит от латинского слова «fractura» с арабским происхождением и означает в переводе: ломать или дробить. Основы теории обыкновенных дробей заложили греческие и индийские математики. Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.
Позже дроби появляются в Европейской математике, например, у Фибоначчи в 1202 году. Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
В России, начиная с древней Руси, дроби именовали долями. А в первых отечественных учебниках по математике дроби назывались ломаными числами. Термин «дробь», как аналог латинского «fractura», впервые используется в «Арифметике» Магницкого в 1703 году как для обыкновенных, так и для десятичных дробей.
Виды дробей
Дроби бывают нескольких видов:
- обыкновенные;
- смешанные и простые;
- правильные и неправильные;
- десятичные;
- в виде процентов.
Обыкновенная дробь
Обыкновенная дробь имеет вид a/b. Число a - здесь будет являться числителем дроби, а число b - будет знаменателем.
Примеры:
- 1/2
- 6/5
- 3/1
- 7/15
Правильные и неправильные
Правильной называется дробь, у которой числитель (модуль числителя) меньше модуля знаменателя.
Пример, правильной дроби: 3/4, так как 3<4.
Неправильная дробь, наоборот, имеет числитель, который по модулю больше чем знаменатель.
Пример, неправильной дроби: 4/3, так как 4>3.
Простые и смешанные
Простая дробь содержит только числитель и знаменатель. Например, 4/3.
Смешанная дробь содержит целое число и дробь, и понимается как сумма этого числа и дроби. Например, 1 и 1/3.
Неправильную дробь всегда можно сделать смешанной, то есть выделить в ней целые части.
Десятичная дробь
Десятичная дробь — это запись дроби, в которой знаменатель не дан в явном виде, но понимается как целое число, степень десяти (напр. 10, 100, 1000 и др).
Десятичная дробь записывается через запятую в строку таким образом, чтобы отделить дробную часть от целой части. Вот так:
- 0,7 – ноль целых и 7 десятых (7/10).
- 5,42 – пять целых и 42 сотых (42/100).
- 9,245 – девять целых и 245 тысячных (245/1000).
В виде процентов
Дробь в виде процентов — это когда при переводе десятичной дроби в проценты, ее необходимо умножить на 100. Запись производится с запятыми.
Например, 0,023 = 0,023 * 100% = 2,3%
Для того чтобы перевести проценты в десятичные дроби, следует разделить число процентов на 100.
Что нужно знать, чтобы работать с дробями?
Что переводить дроби из одного вида в другой и выполнять различные операции над дробями, надо знать несколько терминов.
Наименьшее общее кратное (НОК) для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Наименьший общий знаменатель – это НОК, которое рассчитывается для знаменателей двух и более дробей.
Как найти наименьший общий знаменатель?
Чтобы это понять, необходимо рассмотреть следующий пример двух дробей:
1/20 и 3/14
Если нужно привести дроби с разными знаменателями к общему наименьшему знаменателю, следует найти наименьшее общее кратное (НОК) знаменателей этих дробей.
Знаменатель первой дроби равен 20.
Его нужно разложить его на простые множители: 20=2⋅5⋅2.
Далее также разложить 2 знаменатель дроби 14 на простые множители: 14 = 7*2.
Убираем повторяющиеся множители у знаменателя второй дроби и получаем:
НОК (14,20) = 2*5*2*7 = 140.
В итоге общий наименьший знаменатель равняется 140.
Как привести дробь к общему знаменателю?
Берем первую дробь 1/20 и умножаем ее на 7, чтобы прийти к 140. Для этого умножаем числитель и знаменательно на 7 и получаем:
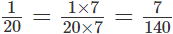
А вторую дробь теперь следует умножить на 10 таким же образом:
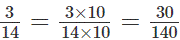
Общим наибольшим делителем (НОД) нескольких чисел является самое большее целое натуральное число, на которое эти самые числа делятся без остатка.
Общий наибольший делитель обозначается в виде такой записи: НОД (18; 48) = 6.
Как следует переводить дробь?
Из смешанной дроби в обыкновенную:
- Необходимо умножить знаменатель дробной части на единицу целой части;
- К произведению, которое получилось, следует прибавить числитель дробной части;
- Сам знаменатель при этом оставить без изменений.
Из обыкновенной дроби в смешанную:
- Разделить числитель дроби на знаменатель;
- Полученный результат будет являться целой частью;
- То, что останется в результате деления (остаток) будет числителем.
Из десятичной дроби в обыкновенную или смешанную^
- Для этого действия необходимо целую часть умножать на знаменатель дробной части.
- После этого полученный результат сложить с числителем дробной части. То, что получилось в итоге, и будет числителем новой дроби, а сам знаменатель при этом останется без изменений.
Операции над дробями
С дробями можно совершать различные арифметические операции.
➕ Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее - выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
Например:
➖ Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
Например:
✖ Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
Например:
➗ Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Например:
📏 Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
Например:
❓ Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них.
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Какие дроби называются десятичными?
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название - десятичные.
Какие дроби называются правильными?
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Какие дроби называются неправильными?
Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.
Как разделить дробь на дробь?
Нельзя делить на 0.
Если делить на 1 - будет такое же число.
Если делить 0 на любое число, получится 0.
Какая дробь называется положительной?
Когда она больше 0.
Какая дробь называется отрицательной?
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Индикт - что это и чему он равен. Индикт — это средневековый период времени, равный 15 годам.
- Декада - это сколько дней. Декада состоит из 10 дней, калькулятор показывает количество дней в декаде.
- Сколько лет в тысячелетии. Введите количество тысячелетий, чтобы узнать, сколько в них лет.
- Сколько месяцев в веке. Введите количество веков, чтобы узнать, сколько в них месяцев.
- Перевести месяцы в года. Введите количество месяцев, калькулятор переведет их в года.
- Перевести годы в недели. Введите количество лет, калькулятор переведет их в недели.
- Перевести недели в дни. Введите количество недель, калькулятор переведет их в дни.
- Перевести дни в недели. Введите количество дней, калькулятор переведет их в недели
- Перевести академические часы в часы. Введите количество академических часов, калькулятор переведет их в часы.
- Перевести наносекунды в миллисекунды. Введите количество наносекунд, калькулятор переведет их в миллисекунды.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии