Площади различных фигур

Рассмотрим методы расчёта площадей различных геометрических фигур, таких как круг, треугольник, прямоугольник, трапеция, а также некоторых объемных (поверхности цилинда, конуса и т.п.).

В этой статье мы исследуем основы геометрии и методы расчёта площадей самых разнообразных фигур. Вы узнаете, как определить площадь каждой из них и как эти знания могут быть применимы в практических задачах.

• Как рассчитать площадь круга?
• Какие существуют способы нахождения площади треугольника?
• Чему равна площадь прямоугольника и как её вычислить?
• Как определить площадь трапеции?
• Как вычисляется площадь поверхности цилиндра?
• Методы расчёта площади поверхности конуса
• Как найти площадь поверхности сферы?
• Как вычислить площадь поверхности усеченного конуса?

Как рассчитать площадь круга?

Круг — одна из наиболее узнаваемых и часто встречающихся геометрических фигур в нашем окружении. От колёс до планет, понимание того, как рассчитывается площадь круга, остаётся важным не только в математике, но и в повседневной жизни.

Площадь круга - это количество пространства внутри круга, которое можно измерить, используя радиус - расстояние от центра круга до его края.

Формула для расчета площади круга является классикой и одной из первых, которую запоминают студенты:

S = πr²

Где S - площадь круга, π (пи) — математическая константа, приблизительно равная 3.14159, а r — радиус круга. Интересный факт: значение π было известно еще древним цивилизациям, и с тех пор оно находит применение в различных областях науки и техники.

💡 Историческая справка. Концепция числа пи (π) была впервые зафиксирована в древнеегипетских и вавилонских записях, что делает её одной из древнейших математических идей, сохранившихся до наших дней.

Знание того, как вычислить площадь круга, помогает не только в учебных задачах, но и в реальных прикладных задачах, таких как планирование земельных участков или дизайн машинных деталей. Это знание необходимо инженерам, архитекторам, дизайнерам и многим другим специалистам.

А тут есть калькулятор площади круга.

Какие существуют способы нахождения площади треугольника?

Треугольник — одна из базовых фигур в геометрии, и способы его измерения могут быть разнообразными. В этом разделе мы рассмотрим несколько методов расчёта площади треугольника, начиная с наиболее простого и широко используемого подхода.

1. Используя высоту и основание

Это самый прямой и часто применяемый метод расчёта площади треугольника. Он основан на следующей формуле:

S = 0.5 * b * h

Где S - площадь треугольника, b - длина основания треугольника, h - высота треугольника, опущенная на это основание.

📐 Шаги к успеху.

1. Измерьте длину основания треугольника.
2. Определите и измерьте высоту, опущенную перпендикулярно к этому основанию.
3. Подставьте значения в формулу и получите результат.

2. Используя две стороны и угол между ними

Этот метод полезен, когда известны две стороны треугольника и угол между ними. Формула для расчёта площади в таком случае выглядит следующим образом:

S = 0.5 * a * b * sin(γ)

Где a и b — длины сторон, а γ — угол между этими сторонами.

🔍 Практические шаги.

1. Измерьте длины двух сторон треугольника.
2. Определите угол между этими сторонами.
3. Используйте значения в формуле для расчёта площади.

3. По трем сторонам (формула Герона)

Если известны все три стороны треугольника, можно использовать формулу Герона для нахождения площади:

S = √(p * (p - a) * (p - b) * (p - c))

Где p — полупериметр треугольника, равный (a + b + c) / 2, а a, b, и c — длины сторон треугольника.

📏 Этапы выполнения.

1. Вычислите полупериметр треугольника.
2. Подставьте значения сторон в формулу и рассчитайте площадь.

Эти методы расчета площади треугольника демонстрируют, что геометрия может быть понятной и доступной, а знания о том, как находить площадь, могут пригодиться в самых разных областях.

А здесь есть калькулятор площади треугольника.

Чему равна площадь прямоугольника и как её вычислить?

Прямоугольник — это четырёхугольник с прямыми углами, что делает его одной из наиболее простых и универсальных фигур в геометрии. Его площадь легко вычислить, и знание этого является основой для решения более сложных задач.

Формула для расчета площади проста:

S = a * b

Где S — площадь прямоугольника, a и b — длины сторон прямоугольника, которые мы называем длиной и шириной соответственно.

📏 Как найти площадь.

1. Измерьте длину одной из сторон прямоугольника.
2. Измерьте длину смежной стороны.
3. Умножьте измеренные значения, чтобы получить площадь.

Эта формула применима не только в теории, но и в повседневной жизни, например, при планировании расположения мебели в комнате или при оценке размера земельного участка.

🧐 Практическое применение. Представьте, что вы хотите купить ковёр для вашей гостиной, чтобы положить его на пол или повестить на стену. Измерив длину и ширину комнаты, вы можете рассчитать, сколько коврового покрытия вам потребуется.

Также стоит помнить, что прямоугольные формы используются не только в строительстве и дизайне. Они встречаются в графическом дизайне, архитектуре, картографии и даже в искусстве.

Зная, как вычислить площадь прямоугольника, вы можете решать задачи, связанные с планированием пространства, оптимизацией использования материалов и эффективностью распределения ресурсов.

В заключение, понимание геометрических принципов площади прямоугольника помогает в создании более функционального и гармоничного пространства вокруг нас.

А тут есть калькулятор площади прямоугольника.

Как определить площадь трапеции?

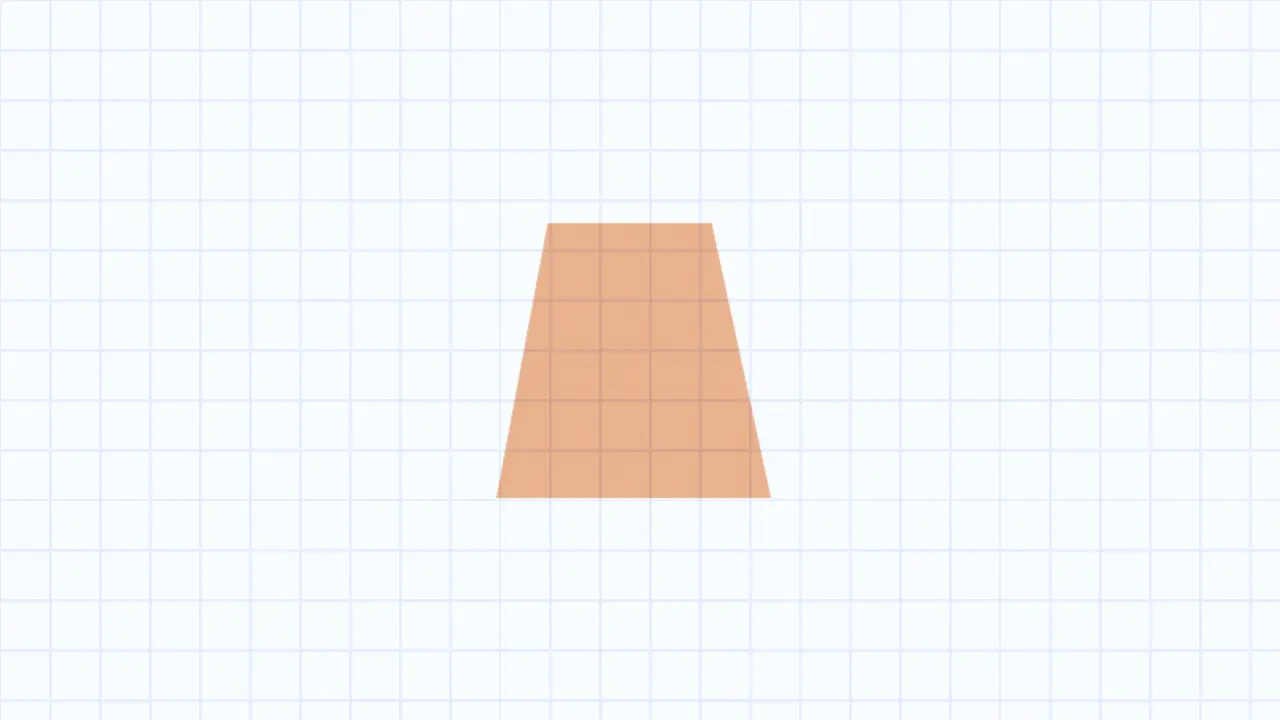
Трапеция — это четырёхугольник, у которого только две стороны параллельны. Именно эта особенность делает расчет её площади немного сложнее, чем в случае с прямоугольником или треугольником.

Формула для расчёта площади трапеции основана на средней линии и высоте:

S = (a + b) / 2 * h

Где a и b — длины оснований трапеции, а h — высота, опущенная перпендикулярно к обоим основаниям.

📐 Как найти площадь.

1. Измерьте длины обоих оснований трапеции.
2. Определите и измерьте высоту трапеции.
3. Подставьте эти значения в формулу для вычисления площади.

Такой метод расчёта применяется в строительстве, где часто приходится сталкиваться с трапециевидными элементами конструкций, такими как крыши, мосты и т.п.

🧐 Практический пример. Представьте, что вы планируете строительство крыши с трапециевидными скатами. Зная площадь каждого ската, можно точно рассчитать необходимое количество кровельных материалов.

Не стоит забывать, что понимание того, как определять площадь трапеции, может быть полезным и в более мелких задачах, например, при проектировании мебели или в дизайне ландшафта.

Эти знания помогают не только сократить расходы на материалы, но и способствуют более эффективному и эстетически приятному использованию пространства.

В заключение, трапеция, хотя и является более сложной фигурой для расчёта, играет важную роль в многих областях человеческой деятельности, и умение правильно рассчитать её площадь открывает новые возможности для реализации творческих и инженерных проектов.

А также можно воспользоваться калькулятором площади трапеции.

Как вычисляется площадь поверхности цилиндра?

Цилиндр — это объёмная фигура, которая играет ключевую роль во многих областях, от машиностроения до архитектуры. Понимание того, как рассчитывается его площадь поверхности, может быть крайне полезным для различных проектов.

Площадь поверхности цилиндра включает в себя площади двух его оснований и боковой поверхности.

Формула для расчёта полной площади поверхности цилиндра состоит из двух частей:

S = 2πr² + 2πrh

Где S — площадь поверхности цилиндра, r — радиус основания, h — высота цилиндра, π (пи) — математическая константа.

📏 Как это работает.

1. Измерьте радиус основания цилиндра.
2. Измерьте высоту цилиндра.
3. Подставьте измерения в формулу, чтобы получить площадь.

Разбив формулу, мы видим, что первая часть (2πr²) относится к площади двух оснований цилиндра, а вторая часть (2πrh) — к площади боковой поверхности, которая представляет собой прямоугольник, образованный при развёртывании цилиндра.

🛠️ Практическое применение. Эта информация особенно важна при расчётах материалов для изготовления труб, баков, бочек и других цилиндрических объектов. Также она необходима при проектировании элементов зданий и различных механических устройств.

Понимание того, как вычисляется площадь поверхности цилиндра, позволяет инженерам и дизайнерам точно определять количество материалов, необходимых для производства, что помогает снижать затраты и увеличивать эффективность проектов.

Научные знания о геометрии цилиндра также могут быть использованы в образовательных целях, помогая студентам лучше понимать объёмные фигуры и их свойства.

В заключение, площадь поверхности цилиндра — это не просто абстрактное математическое понятие, но и важный инструмент в руках профессионалов, работающих в самых разных отраслях.

У нас на сайте есть калькулятор площади поверхности цилиндра.

Методы расчёта площади поверхности конуса

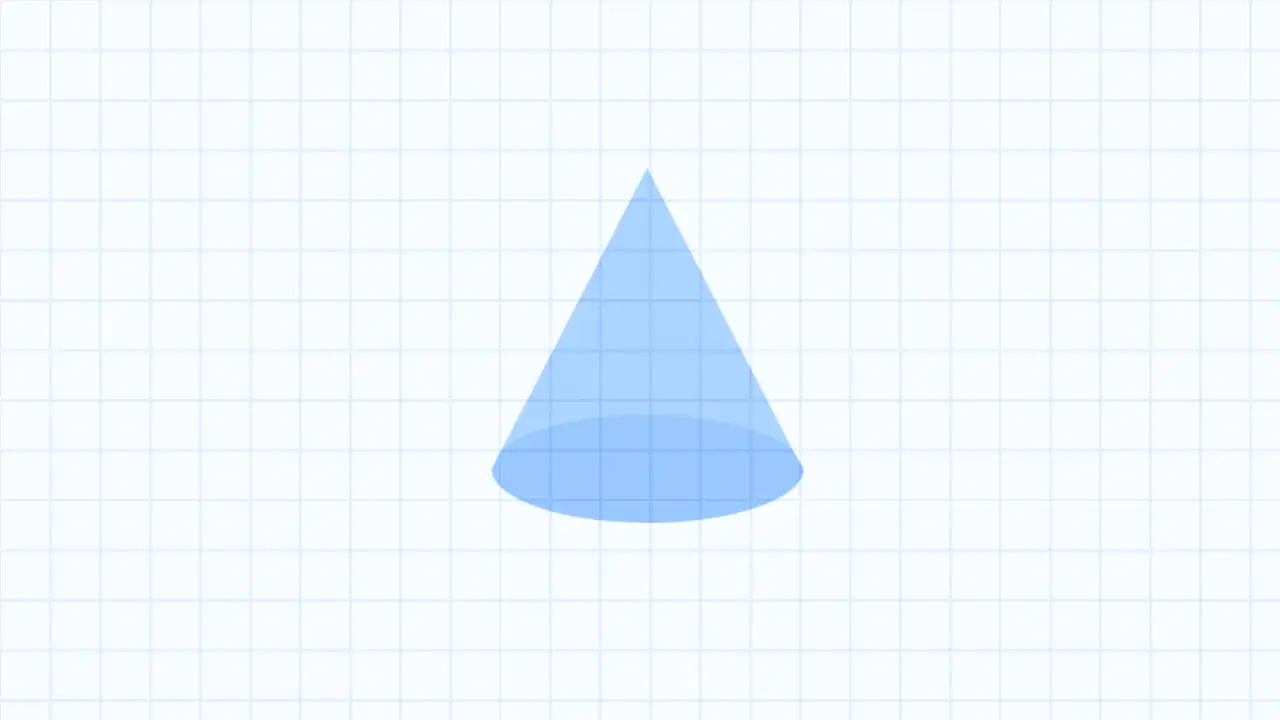
Конус — это объёмная фигура с круглым основанием и вершиной, не лежащей в плоскости основания. Эта геометрическая фигура находит применение во многих сферах, от строительства до аэродинамического дизайна.

Площадь поверхности конуса — это сумма площадей его основания и боковой поверхности, называемой также развёрткой.

Для расчёта полной площади поверхности конуса используется следующая формула:

S = πr(r + l)

Где S — площадь поверхности, r — радиус основания, l — образующая конуса, π (пи) — математическая константа.

📐 Как выполнить расчёт.

1. Измерьте радиус основания конуса.
2. Измерьте длину образующей конуса — расстояние по прямой от вершины до края основания.
3. Подставьте измерения в формулу для нахождения площади.

Эта формула позволяет учитывать как площадь круга основания, так и площадь боковой поверхности, которая представляет собой круговой сектор в развёрнутом виде.

🛠️ Практическое значение. Знание этих расчётов важно при проектировании архитектурных конструкций, например, куполов или при строительстве башен и колоколен.

Также, точные расчёты площади поверхности необходимы при создании макетов и моделей, планировании материальных затрат в производстве и при расчёте стойкости материалов к внешним воздействиям.

В дополнение, знание геометрии конуса помогает в создании более эффективных и экономичных решений в инженерии и технологии.

Таким образом, площадь поверхности конуса не только математически интересный вопрос, но и практически значимый параметр, влияющий на многие аспекты проектирования и производства.

А тут есть калькулятор площади поверхности и объема конуса.

Как найти площадь поверхности сферы?

Сфера — это трёхмерная фигура, каждая точка на поверхности которой равноудалена от центра. Это одна из самых совершенных и гармоничных форм в природе и технике.

Площадь поверхности сферы — это общая площадь, которая покрывает внешнюю сторону сферы.

Для вычисления площади поверхности сферы используется следующая формула:

S = 4πr²

Где S — площадь поверхности сферы, r — радиус сферы, π (пи) — математическая константа.

📐 Как выполнить расчёт.

1. Измерьте радиус сферы.
2. Подставьте радиус в формулу.
3. Вычислите площадь, используя значение π (примерно 3.14159).

Эта формула позволяет легко определить площадь поверхности сфер, что крайне важно во многих технических и научных приложениях.

🛠️ Практическое применение. Знание площади поверхности сферы необходимо в астрономии для расчёта светимости звёзд, в медицине для дозирования лекарств в сферических капсулах, а также в архитектуре и дизайне при создании куполов и других круглых конструкций.

Также, понимание этих расчётов помогает в разработке аэродинамических форм для автомобилей, самолётов и космических аппаратов, где минимизация сопротивления воздуха критична.

В образовательном контексте, изучение площади поверхности сферы способствует глубокому пониманию свойств трёхмерных форм и их практическому применению.

Понимание и правильное использование этой геометрической концепции открывает широкие возможности для научных исследований и инновационных разработок в самых разных областях.

А здесь есть калькулятор площади поверхности сферы.

Как вычислить площадь поверхности усеченного конуса?

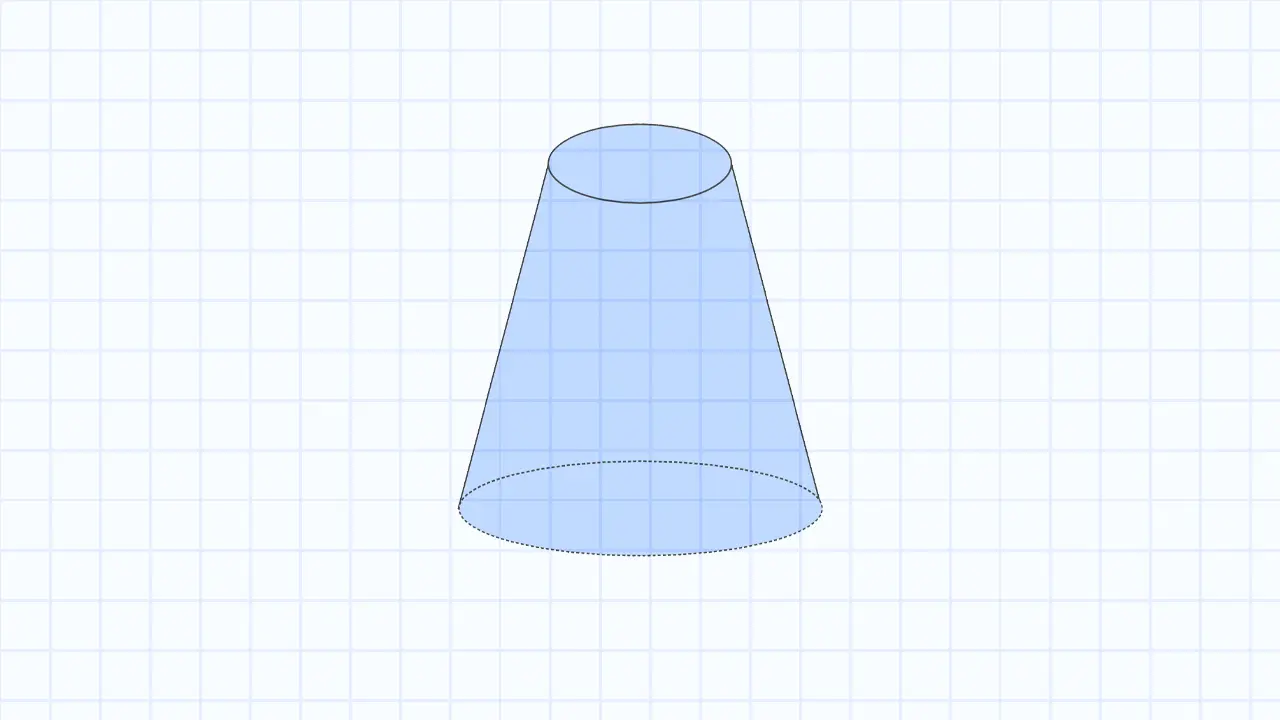
Усечённый конус, или конический слой, — это фигура, получаемая путём сечения конуса плоскостью, параллельной его основанию. Это делает усечённый конус распространённым элементом в архитектуре и инженерии.

Площадь поверхности усеченного конуса — это сумма площадей его двух оснований и боковой поверхности.

Для расчёта площади поверхности усечённого конуса используется формула:

S = π(R + r)l + πR² + πr²

Где S — общая площадь поверхности, R и r — радиусы большего и меньшего оснований соответственно, l — образующая усечённого конуса, π (пи) — математическая константа.

📏 Шаги для расчёта.

1. Измерьте радиусы обоих оснований.
2. Измерьте длину образующей — расстояние по кривой от одного края основания до другого.
3. Подставьте эти измерения в формулу для вычисления площади.

Расчёт площади поверхности усечённого конуса важен при создании различных строительных и машиностроительных проектов, где точность и экономия материалов критичны.

🛠️ Практическое значение. Зная площадь поверхности, можно точно рассчитать количество краски или других покрытий, необходимых для внешней отделки конструкции.

Также эти расчёты используются при проектировании элементов вентиляционных систем, различных типов упаковки, акустических систем и многих других применений, где форма усечённого конуса обеспечивает оптимальные результаты.

В дополнение, понимание свойств усечённого конуса помогает студентам и инженерам в изучении более сложных геометрических и физических концепций.

Таким образом, усечённый конус не только математически интересная фигура, но и важный элемент в практическом инженерном и архитектурном дизайне.

На этой странице есть калькулятор площади поверхности усеченного конуса.

Есть что добавить?

Напишите своё мнение, комментарий или предложение.