Как посчитали число Пи
История и методы вычисления числа Пи, включая приближённые алгоритмы и влияние на науку.
Число Пи, символизирующее отношение длины окружности к её диаметру, остаётся одним из важнейших чисел в математике. В этой статье вы узнаете:
💡 Что такое число Пи?
Число Пи, обозначаемое символом π, является математической константой, указывающей на отношение длины окружности к её диаметру.
Эта константа присутствует во многих формулах в математике и физике, описывая одно из фундаментальных свойств круга.
Другое определение Пи - это отношение полупериода функции y = sin(x) к её максимальному значению, подчёркивающее его связь с тригонометрическими функциями. Здесь x измеряется в радианах; отдельный разбор объясняет, почему π радиан равны 180°.
История числа Пи насчитывает тысячелетия, начиная с древнегреческих исследований и до современных компьютерных алгоритмов. Примечательно, что иррациональность Пи, подтверждённая в 1761 году Иоганном Ламбертом, указывает на его бесконечное и непериодическое десятичное разложение.
Уильям Джонс (1675-1749) - британский математик, который первым использовал греческую букву π для обозначения этой константы. в 1706 году издал работу «Обозрение достижений математики», в которой использовал греческую букву π для обозначения числа «Пи». Символ π был выбран из-за начальной буквы греческих слов περιφέρεια (окружность) и περίμετρος (периметр). Это обозначение было окончательно утверждено после работы Леонарда Эйлера в 1737 году, который подтвердил его использование в научном сообществе.
🔍 Рациональные приближения числа Пи
Рациональные приближения Пи представляют собой попытки выразить значение числа Пи с помощью дробей (где в числитете целое, а в знаменателе натуральное число), которые, хотя и не точны, дают удивительно близкие результаты к истинному значению.
Самым известным примером такого приближения является дробь 22/7, предложенная Архимедом. Это приближение было результатом его метода вписывания и описывания многоугольников вокруг окружности.
Другой знаменитый рациональный приближитель - 377/120, полученный Клавдием Птолемеем, древнегреческим астрономом и географом. Эта дробь давала еще более точное приближение числа Пи и использовалась в астрономических расчетах.
Цзу Чунчжи, китайский астроном и математик, предложил приближение 355/113, которое оказалось еще точнее и до сих пор считается одним из лучших однозначных рациональных приближений числа Пи.
Эти приближения важны не только из-за своей практической ценности для вычислений, когда доступ к высокоточным инструментам ограничен, но и потому что они позволяют лучше понять свойства Пи как иррационального числа.
Сравнение точности различных приближений показывает, как развивалось понимание числа Пи со временем:
- 22/7 - Округленное значение: 3,142857, точность до двух знаков после запятой.
- 377/120 - Округленное значение: 3,141667, точность до трех знаков после запятой.
- 355/113 - Округленное значение: 3,141593, точность до шести знаков после запятой.
Каждое из этих приближений вносило свой вклад в математику, позволяя ученым с разных уголков мира вносить свой вклад в развитие науки о числах и, в частности, о Пи.
📐 Геометрический период в исследовании числа Пи
Исследование числа Пи, символа, ставшего ключом во многих геометрических теориях, начинается с древности. Этот период характеризуется попытками понять и вычислить Пи через геометрические построения.
Уже древние цивилизации, такие как египтяне, вавилоняне и греки, понимали, что отношение длины окружности к диаметру одинаково для всех окружностей и примерно равно 3. Это знание было записано и передано через тысячелетия. Практическое применение формулы показывает инструкция по измерению диаметра трубы обычной лентой.
Архимед, великий геометр древности, внёс значительный вклад в вычисление Пи. Он использовал метод правильных многоугольников, вписывая их в окружность и описывая около неё, чтобы находить приближённые значения Пи.
С его помощью, рассматривая правильные 96-угольники, Архимед пришёл к выводу, что Пи заключено между 310/71 и 31/7, и предложил использовать значение 22/7 для приближённых расчётов.
Другой важный вклад внёс Клавдий Птолемей, который разработал таблицу хорд и с её помощью получил для Пи значение 377/120. Это значительно улучшило понимание геометрических свойств окружности в рамках астрономии.
В Китае, математик Лю Хуэй применил метод последовательных приближений с помощью 96-угольника, благодаря чему смог уточнить значение Пи до 3,1416. Этот метод основывался на принципе, что площади многоугольников, следующих друг за другом, уменьшаются в геометрической прогрессии.
Таким образом, геометрический период в истории Пи подчеркивает его универсальность и значимость не только в математике, но и в астрономии и других науках, где точные измерения играют ключевую роль.
Эти ранние методы и теории легли в основу будущих математических открытий, подтверждая, что даже с древними инструментами учёные могли приближаться к пониманию сложных природных закономерностей.
🕰 Классический период изучения числа Пи
Классический период открыл новую эру в исследованиях числа Пи, когда математики начали использовать инструменты математического анализа для достижения невероятной точности в его вычислениях.
До начала этого периода известно было всего около десяти точных цифр Пи. Однако с развитием математического анализа в XVII веке ситуация кардинально изменилась.
Одним из революционных подходов стало использование бесконечных рядов, которые позволяли вычислять Пи с любой желаемой точностью, добавляя все больше членов ряда.
Мадхава из Сангамаграмы, математик из Индии, сделал значительный прорыв, разработав серии таких рядов. Один из его рядов, известный как ряд Мадхавы-Лейбница, позволял пошагово приближаться к точному значению Пи.
Европейский вклад внёс Людольф ван Цейлен, который посвятил многие годы уточнению цифр Пи, достигнув 20 точных знаков, что на тот момент было рекордным достижением.
Интересный вклад в историю Пи внесли также Лейбниц и Эйлер, которые использовали свои знания для разработки формул, связывающих Пи с другими математическими концепциями и функциями, что расширило понимание его свойств.
Исследования Пи в этот период также включали уточнение его иррациональной и трансцендентной природы. Легендарное доказательство трансцендентности Пи, предложенное Фердинандом фон Линдеманом в 1882 году, окончательно подтвердило, что Пи невозможно выразить с помощью любого алгебраического уравнения с рациональными коэффициентами. Разница между рациональными, иррациональными, алгебраическими и трансцендентными числами подробно объяснена в статье о видах чисел.
Этот период подчеркивает, как глубоко Пи встроено в структуру математики и как значительно продвинулось понимание его характеристик благодаря усилиям учёных разных эпох.
🌐 Эра компьютерных вычислений числа Пи
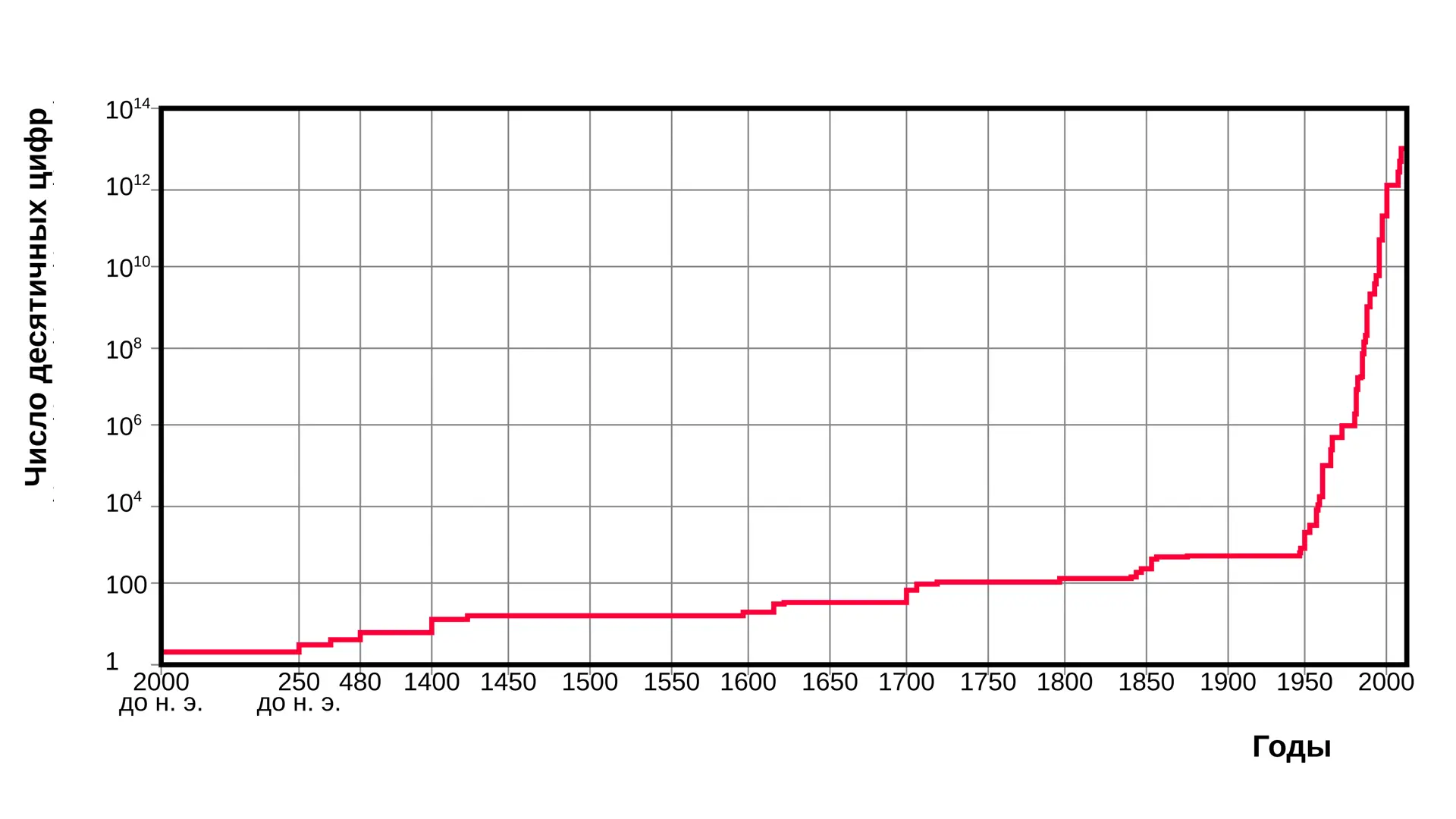
С развитием компьютерных технологий XX века, точность вычислений числа Пи достигла невероятных высот. Джон фон Нейман и его коллеги в 1949 году использовали компьютер ENIAC для вычисления 2037 цифр Пи, что стало значительным прорывом в истории вычислительной математики.
С течением времени, методы стали еще более изощренными. Например, формула Белларда, разработанная в 1997 году, позволяла вычислять биты Пи независимо друг от друга, что значительно ускоряло процесс при использовании параллельных вычислений.
Формула Бейли - Боруэйн - Плаффа, открытая в 1997 году, стала еще одним важным инструментом, который доказал свою эффективность благодаря своей способности вычислять цифры Пи последовательно и без необходимости вычисления предыдущих значений.
Компьютерная эра также привнесла рекорды по количеству вычисленных знаков Пи. В 1989 году братья Чудновские достигли нового рекорда, вычислив 1 миллиард цифр Пи, используя свою собственную разработанную формулу.
В 2002 году был установлен новый рекорд - 1.24 триллиона цифр, что было возможно благодаря алгоритмам, использующим суперкомпьютеры, способные обрабатывать огромное количество операций за секунду.
Развитие технологий привело к еще более значимым достижениям, например, в 2019 году Google представила число Пи с точностью до 31.4 триллиона знаков, используя инфраструктуру облачных вычислений для достижения этого результата.
К 2021 году, благодаря прогрессу в области суперкомпьютеров, ученые смогли вычислить Пи с точностью до 62.8 триллиона знаков после запятой, каждый раз устанавливая новые стандарты для будущих поколений ученых.
Эта эпоха не только продемонстрировала мощь современных технологий, но и открыла новые перспективы в изучении математических констант, продолжая вдохновлять математиков и инженеров по всему миру.
А с помощью данной формы вы сможете посчитать число пи с точностью до 10 тыс. знаков.
Есть что добавить?
Напишите своё мнение, комментарий или предложение.