Ахиллес и черепаха
Одна из апорий древнегреческого философа Зенона утверждает, что Ахиллес никогда не догонит черепаху. Исследуем, так ли это и когда же он её догонит.
Задача Ахиллеса и черепахи - классический пример парадокса, представленного древнегреческим философом Зеноном. Эта статья расскажет вам о деталях парадокса и его анализе на примере математики и физики. Вы узнаете:
Что такое парадокс (апория) Ахиллеса и черепахи: простыми словами
В апории о Ахиллесе и черепахе Зенон рассуждает так: если Ахиллес дает черепахе фору, то, несмотря на свою скорость, он никогда не сможет ее догнать. Каждый раз, достигая точки, где была черепаха, Ахиллес обнаруживает, что черепаха уже переместилась вперед.
Парадокс Ахиллеса и черепахи — это одна из знаменитых апорий древнегреческого философа Зенона Элейского, задуманная для демонстрации, как простые логические предположения могут привести к неожиданным и абсурдным выводам.
Зенон Элейский (около 490—430 гг. до н. э.) — древнегреческий философ, известный своими парадоксами, направленными на критику многовековых философских учений о множественности и изменчивости бытия.
Апория — это философский термин, означающий затруднение или неразрешимую логическую проблему, которая подразумевает столкновение двух одинаково обоснованных, но логически несовместимых утверждений.
Этот парадокс демонстрирует некоторые несовершенства классической логики, показывая, что логические рассуждения могут заводить в тупик и расходиться с реальностью. Он заставляет задуматься о пределах нашего понимания бесконечности и непрерывности.
Именно такие размышления Зенона оставляют значительный след в истории философии, предоставляя бесценный материал для обсуждения вопросов времени, пространства и бесконечности.
Почему же Ахиллес не может догнать черепаху согласно Зенону
Парадокс Ахиллеса и черепахи, предложенный Зеноном, иллюстрирует наглядный пример бесконечного деления времени и пространства, что приводит к кажущемуся парадоксу.
Согласно античной логике, Ахиллес, самый быстрый из бегунов, дает фору медлительной черепахе. Исходя из условий, даже если Ахиллес в десять раз быстрее черепахи, он начинает забег с определенного отставания.
- Ахиллес должен сначала добраться до того места, где изначально была черепаха.
- За это время черепаха продвигается вперед, хоть и небольшое расстояние.
- Каждый раз, достигая точки, где только что была черепаха, Ахиллес видит, что она снова немного опередила его.
Таким образом, каждое последующее действие Ахиллеса только приближает его к черепахе, но не позволяет догнать ее окончательно, формируя бесконечную последовательность событий.
Исторически, этот парадокс впервые упоминается Аристотелем в его труде «Физика», где он описывает аргументы Зенона о невозможности достижения одного объекта другим, если последний начинает с отставания.
Диоген Лаэртский, знаменитый историк, приписывает создание этого парадокса Пармениду, учителю Зенона, хотя более поздние комментаторы, такие как Симпликий и Фемистий, внесли свои коррективы, добавив образ черепахи.
Эта апория стала одной из основ для размышлений о природе движения и времени, став ключевым аргументом в дебатах о бесконечной делимости пространства и времени.
Многие попытки решения этого парадокса в современной математике, использующие концепцию сходящихся рядов, представляют собой интересные, но все же упрощенные модели реальных процессов. Зенон, вероятно, стремился показать, что даже при применении математических моделей, идеальные понятия могут не соответствовать реальности.
Так, апория о Ахиллесе и черепахе остается актуальной, поднимая вопросы о сущности времени и пространства, и доказывая, что философские размышления могут найти отражение в самых неожиданных областях знаний.
Как математика объясняет и опровергает этот парадокс
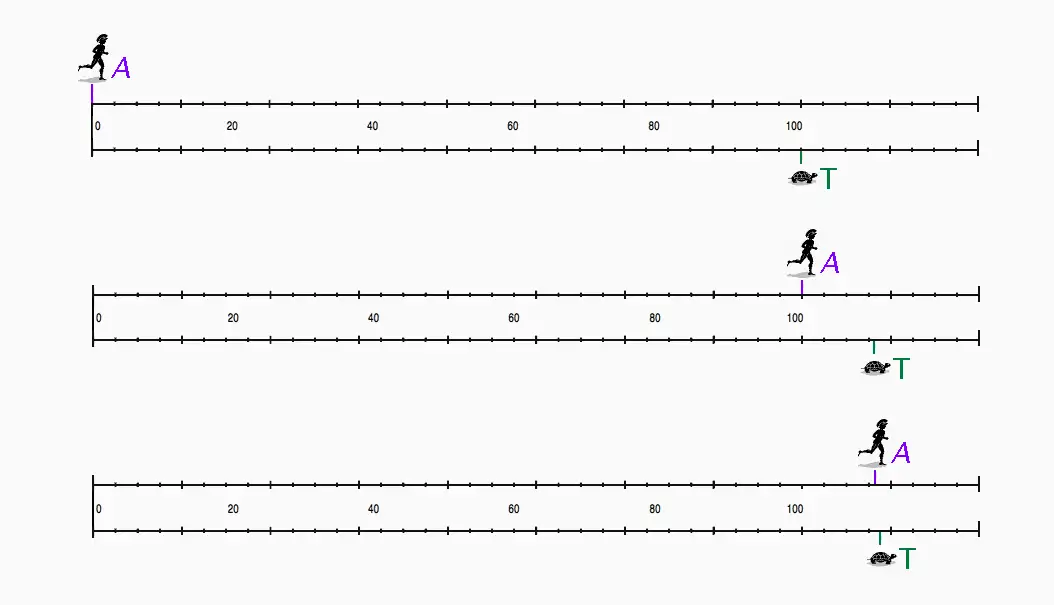
Математика предлагает элегантное решение парадокса Ахиллеса и черепахи, используя концепцию пределов и суммы геометрической прогрессии, чтобы показать, как Ахиллес в итоге догоняет черепаху.
Рассмотрим последовательность событий, когда Ахиллес пытается догнать черепаху: Ахиллес бежит 100 метров и за это время черепаха продвигается на 1 метр. Когда Ахиллес пробегает эти дополнительные 1 метр, черепаха успевает проползти 0.01 метра, и так далее.
Эту последовательность можно представить как сумму геометрической прогрессии:
100 + 1 + 0.01 + 0.0001 + ...
Где каждый следующий член прогрессии меньше предыдущего в 100 раз. Эта прогрессия имеет вид:
a / (1 - r)
где a = 100 (первый член), r = 0.01 (знаменатель).
Подставляя значения, получаем:
100 / (1 - 0.01) = 100 / 0.99 ≈ 101.01
Таким образом, Ахиллес догонит черепаху примерно на 101.01 метре.
Этот расчет демонстрирует, как математический предел помогает преодолеть парадоксальность ситуации, созданной бесконечным уменьшением расстояний. Благодаря концепции пределов, бесконечная последовательность событий фактически приводит к конечному результату.
Введение предела в анализ позволяет показать, что хотя каждое последующее действие приближает Ахиллеса к черепахе на величину, стремящуюся к нулю, сумма этих бесконечно малых шагов имеет вполне определенное и конечное значение.
Такой подход не только решает парадокс Зенона в математическом плане, но и предоставляет интуитивное понимание бесконечных процессов, подчеркивая значимость пределов для анализа кажущихся неразрешимыми ситуаций.
Исследование таких философских проблем с помощью математических инструментов показывает глубину и применимость математического анализа к абстрактным и практическим вопросам науки и жизни.
В чём философский смысл этого парадокса
Парадокс Ахиллеса и черепахи выходит за рамки математической загадки, затрагивая глубокие философские темы о природе реальности, времени и движения. Рассмотрим ключевые аспекты философского смысла этой апории.
🧠 Пределы познания. Зенон через свои парадоксы пытался показать ограниченность человеческого понимания и способности наших сенсорных и когнитивных систем адекватно воспринимать бесконечность и непрерывность.
🌀 Иллюзорность движения. Зенон использует парадокс, чтобы поставить под сомнение саму возможность движения, предполагая, что то, что мы воспринимаем как движение, на самом деле может быть иллюзией, разбиваемой на бесконечное количество моментов покоя.
🕰 Бесконечность пространства и времени. Парадокс поднимает вопросы о структуре пространства и времени. Он демонстрирует, что понятия бесконечности и деления на бесконечно малые части могут привести к логическим противоречиям.
📚 Критика эмпиризма. Апория вызывает сомнения в достоверности наших непосредственных эмпирических ощущений и опыта, предлагая, что наша эмпирическая реальность может быть искажена или ограничена.
🔗 Метафизика идентичности. Парадокс заставляет задуматься над вопросами идентичности и изменчивости объектов во времени, что является центральным в метафизических дебатах о том, что остаётся постоянным в процессе изменения.
🎭 Влияние на современную философию. Рассуждения Зенона оставили значительный след в философии, влияя на такие направления, как феноменология, постструктурализм и деконструкция, каждое из которых переосмысливает понятия времени и реальности.
🌌 Теоретическая физика. Идеи, заложенные в парадоксе, находят отклики в современной теоретической физике, в частности, в теории относительности и квантовой механике, где понятия времени и пространства также подвергаются пересмотру.
Таким образом, парадокс Ахиллеса и черепахи, оставаясь казалось бы простой логической загадкой, открывает глубокие философские измерения и продолжает вызывать живой интерес и дебаты в философском сообществе. Но одно остаётся бесспорным - бегать нужно в своём темпе, для этого мы я сделал на ecalc специальный калькулятор темпа бега.
Какие еще апории Зенона известны
Зенон Элейский оставил после себя несколько апорий, каждая из которых ставит под сомнение общепринятые представления о действительности, времени и пространстве. Рассмотрим некоторые из наиболее известных апорий, которые продолжают вызывать интерес у философов и ученых.
🏁 Дихотомия. Эта апория утверждает, что прежде чем достичь конечной точки, необходимо достичь половины пути, а перед этим — половины от половины и так до бесконечности. Таким образом, движение кажется невозможным, так как всегда остается еще один шаг, который нужно выполнить.
🔁 Стрела. В этой апории Зенон аргументирует, что летящая стрела в каждый конкретный момент времени находится в состоянии покоя, поскольку она не перемещается в этот точный момент. Если время состоит из мгновений, в каждый из которых стрела неподвижна, то, следовательно, она и весьма неподвижна.
🌌 Стадион. Эта апория демонстрирует противоречие, возникающее при рассмотрении двух рядов объектов, движущихся мимо третьего ряда с одинаковой скоростью в противоположных направлениях. Зенон утверждает, что должно получаться, что один ряд движется вдвое быстрее другого, хотя скорость у них одинаковая.
🌀 Бегущие. Похож на парадокс Ахиллеса и черепахи, этот парадокс утверждает, что быстрый бегун не может догнать медленного, если последний начал бег с форы, так как быстрый всегда будет достигать точку, которую медленный уже покинул.
Эти апории Зенона используют различные аспекты бесконечности и непрерывности, чтобы вызвать сомнения в интуитивных представлениях о движении и времени. Их значимость для философии и науки трудно переоценить, так как они задают фундаментальные вопросы о природе реальности.
Апории Зенона оказали значительное влияние на развитие логики и математики, подталкивая к разработке теорий бесконечно малых и пределов, которые легли в основу современного математического анализа.
Философский вызов, который Зенон представил через свои парадоксы, продолжает быть предметом активного исследования и обсуждения, подчеркивая не только сложности понимания бесконечности, но и нашу способность критически оценивать и интерпретировать феномены действительности.
Изучение апорий Зенона подчеркивает важность критического мышления в научных и философских дисциплинах, а также их взаимосвязь, демонстрируя, как философские задачи могут стимулировать научные открытия и теоретические инновации.
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии